机器学习中优化相关理论基础汇总

2019年04月30日 13:14:53  阅读数 131更多

分类专栏： 

 

版权声明：本文为博主原创文章，遵循版权协议，转载请附上原文出处链接和本声明。

本文链接：

在阐述机器学习中优化所需相关理论基础前，既然是谈机器学习算法，我们先了解一下机器学习中算法分类：

1、监督学习：训练数据每个实例都带有label

2、非监督学习：训练数据没有label

3、强化学习：与监督学习和非监督学习并列的第三类机器学习算法

4、弱监督学习：分为三种 不完全监督、不确切监督、不准确监督

5、半监督学习：由于标注数据困难等原因，只有部分数据含有label

6、多示例学习：每个数据包含有label，但每个数据包中含有多个数据实例，每个实例在训练的时候不存在label，数据包中有一个数据为正则数据包标签为正，数据包中实例全部为负则数据包标签为负

一、什么是优化，常见的优化形式

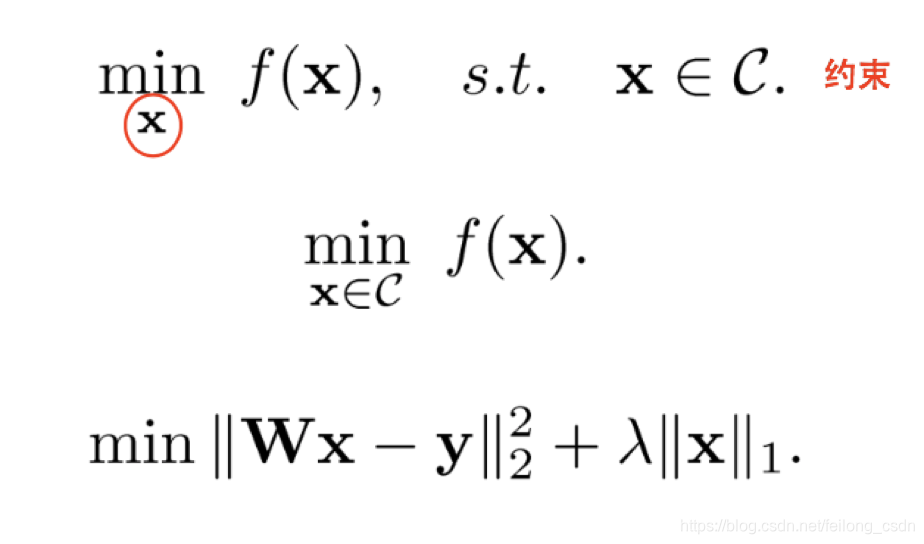
二、优化问题分类

常见分类:

1、连续优化问题： solution set is continuous

2、离散优化问题：solution set is discrete

3、组合优化问题：solution set is finete

4、变分优化问题：solution set is infinite dimensional subset of a space of functions

5、多任务优化问题

6、多层次优化问题

7、分类优化问题

基于约束的优化问题分类:

1、unconstrained

2、equality constrained

3、inequality constrained

基于目标函数的优化问题分类:

1、convex programs

2、linear programs

3、quadratic programs

4、semi-definite programs

5、second-order cone programs

6、non-convex programs

7、sparse/low-rank models

8、polynomial programming

9、fractional programming

三、优化问题需突破方面

1、Smooth -> Nonsmooth ：从平滑到非平滑

2、Convex -> Nonconvex ： 从凸到非凸

3、One/Two Block -> Multi Blocks ： 从单块到多块

4、Deterministic -> Stochastic ： 从确定到随机

5、Synchronous -> Asynchronous ： 从同步到异步

6、Centralized -> Decentralized ： 从集中到分散

7、Improved Convergence & Convergence Rate ： 提高收敛性和收敛速度

四、向量范数和矩阵范数

向量范数:

p范数是二范数的拓展，其中 p∈[1,inf)，距离定义是一种宽泛的概念，主要满足非负，自反和三角不等式就可以称之为距离，范数是一种强化了的距离概念，比距离多了一条数乘的运算法则，因为可以吧范数当成距离来理解，在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表示矩阵引起变化的大小，下面给出常见的向量范数

1、P范数，p范数不是一个范数，而是一组范数

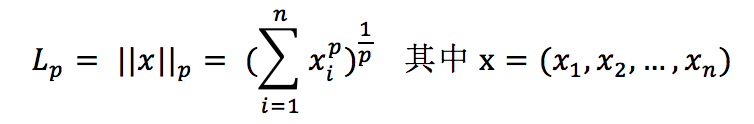下图表示了p从∞到0的变化，三维空间中到原点的范数(距离)为1的点构成的图形的变化情况，常见的二范数即是欧式距离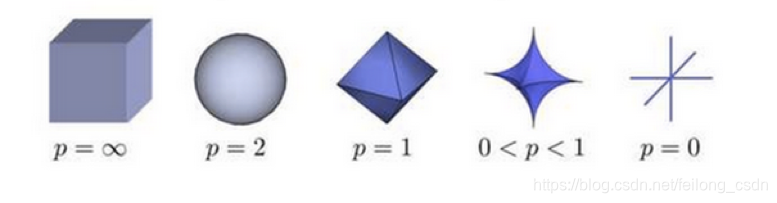

2、L0范数：表示向量x中非零元素的个数

3、L1范数：表示向量x中非零元素的绝对值之和

4、L2范数：度量欧式距离

5、范数：度量向量元素的最大值

矩阵范数:

把矩阵看作线性算子，那么可以有向量范数诱导出矩阵范数：

会自动满足对向量范数的相容性

常见的三种p-范数诱导出的矩阵范数为：

1、矩阵1-范数： 列和范数，矩阵A的每一列元素绝对值之和的最大值

2、矩阵2-范数： A的最大奇异值，即的特征值中最大特征值的平方根，其中为A的共轭矩阵：

3、矩阵∞-范数： 行和范数，矩阵A每一行元素绝对值之和的最大值

矩阵条件数，条件数也分为1条件数，2条件数和无穷条件数，条件数定义为矩阵的范数乘以矩阵的逆矩阵的范数：

矩阵的条件数总是大于1，正交矩阵的条件数总是等于1，奇异矩阵的条件数总是无穷大，当这里取二范数时，矩阵条件数等于矩阵A的极大奇异值除以A的极小奇异值

五、优化问题中相关概念定义

1、NFL定理 No-free-lunch定理

没有Universally的算法，算法好坏的比较需要基于具体的问题

2、序列Sequences：单调有界序列必收敛

3、上确界Supremum：一个集合A的最小上界

4、下确界infimum：一个集合E的最大下界

5、极限limit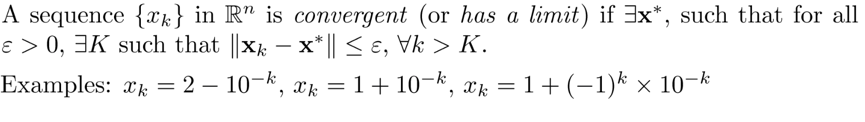

6、聚点Accumulation point：聚点周围任意小的区间，都有无穷多个点，集合A所有聚点的集合称为A的导集

7、致密性定理Bolzano-Weierstrass theorem：有界数列必有收敛子数列

8、全局收敛和局部收敛Global and local convergence

全局收敛：凸优化问题往往全局收敛

局部收敛：一定范围内收敛

9、收敛速率Convergence rate，下面给出收敛速率的定义

r是收敛速率，当r=1时，线性收敛

当r=2时，Quadratic收敛

当r=3时，Cubic收敛

给出收敛速度r的估计：

10、函数的连续性定义Continuity

11、全局最小和局部最小Minimum and minimal

Minimum point：全局最小点、Minimal point：局部最小点

12、函数相关性质

(1) Closedness

(2) Derivative

(3) Gradient

(4) Chain rule

(5) Second derivative

(6) Chain rules for second derivative

13、两个重要矩阵

(1) Jacobian

(2) Hessian

14、集合相关定义

(1) 开集Open set： ()

(2) 闭集Close set： []

(3) 有界集Bounded set：集合是有界的

(4) 紧集Compact set： 有界且闭 bounded set + close set

(5) 内点集Interior：包含于集合的最大开集

(6) 闭包Closure：包含于集合的最小闭集

(7) 边界Boundary：闭包-内点集

15、向量标准内积Inner product

16、函数f被称为norm需要满足以下四个条件：非负、确定、齐次、三角不等式

17、特征值分解Symmetric eigenvalue decomposition

18、奇异值分解Singular Value Decomposition: 特征值分解和奇异值分解详细分析请参看博文：

机器学习算法中优化基础知识相关概念笔记，供参考！